福野泰介の一日一創

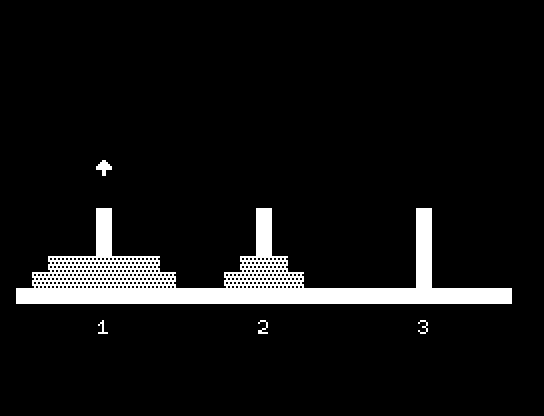
「ハノイの塔/Kidspod;」 by 永谷 弘宣氏

左のピンから右のピンへ円盤を移せばOK。
1度に動かせるのは1枚だけ。
小さな円盤の上に大きな円盤は載せられません。

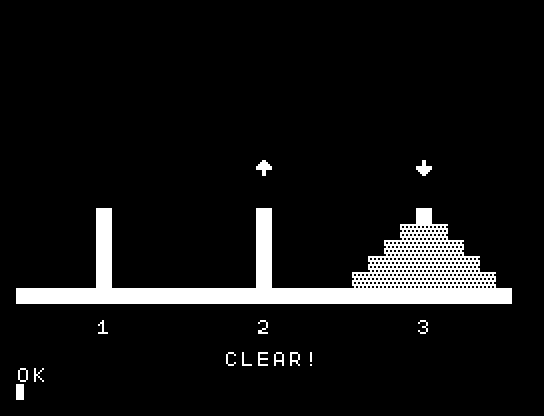
クリア！

コツはつかめましたか？

円盤4枚のハノイの塔、実はミニバージョン。
ベトナム、ハノイの伝説では、円盤64枚だそうです。
手で動かすのは大変そうなので、コンピューターに手順を教えてやってもらいましょう。

円盤の数が1枚の円盤を動かすときは簡単、左から右へ移すだけ。
2枚のときは、一番上の1枚を使わないピンに退避して、2枚目を右へ移し、退避したものを右へ移す。
n枚動かすときは、n-1枚を使わないピンに退避して、n枚目を目的のピンへ移し、退避したものを目的のピンへ移す。

こういう自己再利用的な考え方を、再帰的アルゴリズムと呼びます。（再帰 - Wikipedia）

IchigoJamでハノイの塔の解法を表示させてみましょう。
IchigoJam BASICにおける再帰的アルゴリズムでは、配列をスタックとして使って変数とします。

10 @HANOI 20 IF[S-4]=0:S=S-4:RTN 30 LET[S],[S-4]-1,[S-3],[S-1],[S-2]:S=S+4:GSB@HANOI 40 ?[S-4];": ";[S-3];" -> ";[S-2] 50 LET[S],[S-4]-1,[S-1],[S-2],[S-3]:S=S+4:GSB@HANOI 60 S=S-4:RTN

スタックに、円盤の枚数、動かす元のピン番号、動かす先のピン番号、余りのピン番号と、4つ積み、@HANOIを呼び出します。

LET[0],1,1,3,2:S=4:GSB@HANOI 1: 1 -> 3

1枚だけ

LET[0],2,1,3,2:S=4:GSB@HANOI 1: 1 -> 2 2: 1 -> 3 1: 2 -> 3

2枚

LET[0],3,1,3,2:S=4:GSB@HANOI 1: 1 -> 3 2: 1 -> 2 1: 3 -> 2 3: 1 -> 3 1: 2 -> 1 2: 2 -> 3 1: 1 -> 3

3枚・・・と、どんどん手数が増えていきますね。
4枚の時の計算をしてメモし、実際にハノイの塔で解いてみましょう。

5枚の時の手順は？
6枚の時の手順数は？
64枚ではどのくらいになるでしょう？

京が64枚のハノイの塔を解くのにかかる時間はどのくらい？
（1秒で1京計算できるスパコン、1回の動きが1計算で完了することとします）

参考に、再帰的アルゴリズムを使った他のアルゴリズムの紹介です。

最大公約数
二つの数、どんどん余りの計算をして割り切れたときの割った数が最大公約数（ユークリッドの互除法）。

10 @GCD 20 IF[S-1]=0:S=S-1:RTN 25 ?[S-2];", ";[S-1] 30 LET[S],[S-1],[S-2]%[S-1]:S=S+2:GSB@GCD 40 [S-3]=[S-1]:S=S-2:RTN LET[0],1920,1080:S=2:GSB@GCD:END

階乗
その数より小さい正数を全部かけたものが階乗。

10 @FACT 20 IF[S-1]=0:[S-1]=1:RTN 30 [S]=[S-1]-1:S=S+1:GSB@FACT 35 ?[S-2];"*";[S-1];"=";[S-2]*[S-1] 40 [S-2]=[S-2]*[S-1]:S=S-1:RTN [0]=7:S=1:GSB@FACT:?[0]

フィボナッチ数
0,1から始まり、ふたつ前の数を足した数が連なるのがフィボナッチ数列。

10 @FIB 20 IF[S-1]<2:RTN 30 [S]=[S-1]-1:S=S+1:GSB@FIB 40 [S]=[S-2]-2:S=S+1:GSB@FIB 45 ?[S-2];"+";[S-1];"=";[S-2]+[S-1] 50 [S-3]=[S-2]+[S-1]:S=S-2:RTN [0]=10:S=1:GSB@FIB:?[0]

スタックは、身につけておきたい、メモリの便利な使い方です！

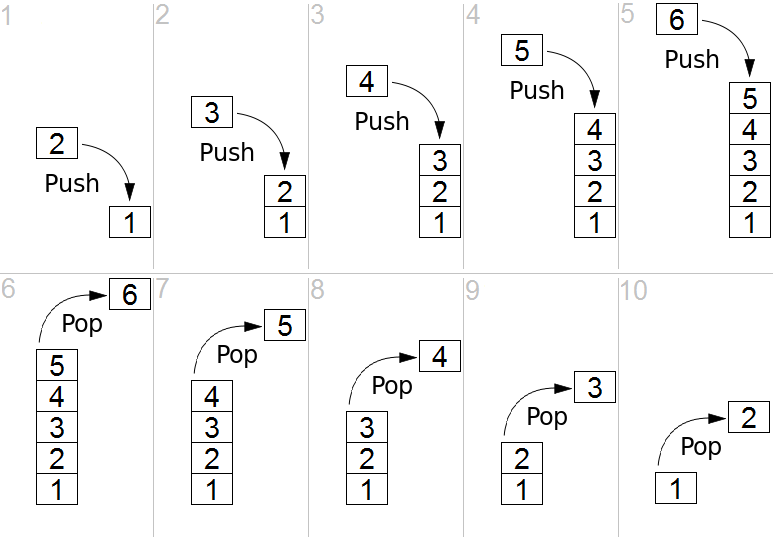
スタック - from Wikipediaより

※各種小改良した、IchigoJam BASIC ver 1.2.4予定のbeta56、IchigoJam-FANにて紹介中です！

links
- IchigoJamで学ぶデータ構造「スタック」
- ハノイの塔/Kidspod;
- IchigoJam-FAN - Facebook