「プログラミングで学ぶ、安全安心なまちに必須の暗号化技術「さいきょうのあんごうワンタイムパッド」」
ワンタイムパッド暗号の鍵の受け渡しに、いつ誰が見ているかわからないインターネットは使えません。直接会って手渡しするか、厳重に封をして書留で送るなど、別の経路が必要になって手間がかかります。
信用できない通信路だけで、信用できる通信をする方法はないものか?実はあるんです。その最新の技術がECDH(楕円曲線ディフィー・ヘルマン鍵共有)です。 楕円曲線上の離散対数問題が、現代の知識とコンピューターでは現実的な時間で解けないという、数学を利用した鍵共有方法です。
Web標準の Web Crypto API を使って、実際試してみました。
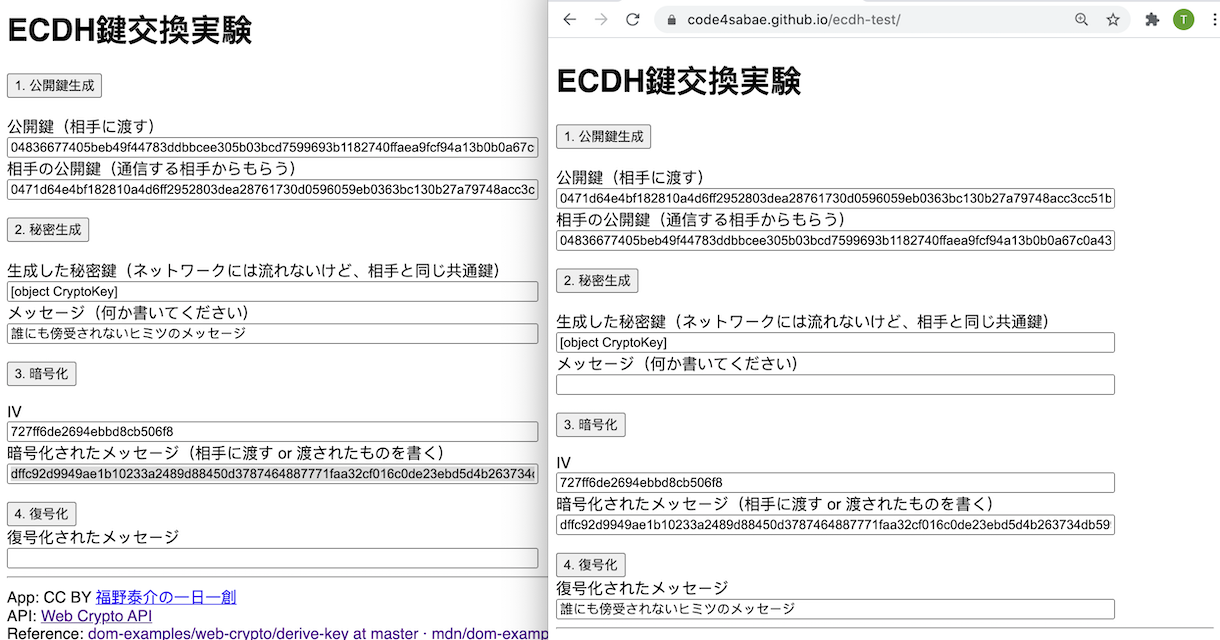
「ECDH鍵共有実験 - Web Crypto API」(src on GitHub)
上記を2つブラウザで開きます。離れたところにいる誰か友達に開いてもらってもOKです。まず、お互い公開鍵を生成し、相手に公開鍵を送信し合い、受け取った、公開鍵をセットします。
自分で生成した鍵と受け取った公開鍵から、実際に暗号化、復号化に使う共通鍵が生成できます。
この共通鍵、ネットワークでやりとりせずに、2つ(2人)で全く同じであるところがおもしろいところです! 通信路の二人の公開鍵から共通鍵を計算することが事実上不可能であることが信用の担保となっています。(もし計算できたら世界的な大発見になるので、それはそれでぜひチャレンジしてください)
共通鍵が共有できたので、あとはこれを使って暗号化するだけです。今回は AES-GCM というアルゴリズムを使って、暗号化していますが、ワンタイムパッドとして使うのもありですね。
この技術のおかげで、インターネットで安心してショッピングしたり、メッセージを送り合ったりできているわけです。 本人確認、本人認証と組み合わせて、確定申告など、電子申請にも使用されています。
でも、安心は禁物。楕円曲線上の離散対数問題をシンプルに解く新アイデアや技術が登場しない保証はありません。 コンピューターは速くなりつづけ、増え続けるので、力づくで解読できてしまう日もきっと来ます。
新技術、楽しくウォッチしていきましょう!
みんなでつくるDX、DXGOV#3は、10/22木15:30-17:30 オンライン開催!

